对数函数的图像,图像解析与奥秘揭示
你知道吗?在数学的世界里,有一种神奇的函数,它就像一个魔法师,能将复杂的数字变得简单易懂。它就是——对数函数!今天,就让我带你一起探索对数函数的图像,看看它那独特的魅力吧!
一、对数函数的起源
对数函数的历史悠久,最早可以追溯到古希腊时期。不过,真正让对数函数成为数学界宠儿的是17世纪的英国数学家约翰·纳皮尔。他发明了对数,使得计算变得简单快捷。而今天,对数函数已经成为数学、物理、工程等领域不可或缺的工具。
二、对数函数的定义
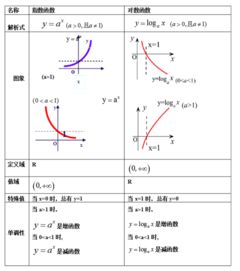
对数函数的定义是这样的:如果\\(a^x = b\\),那么\\(x\\)就是\\(b\\)以\\(a\\)为底的对数,记作\\(x = \\log_a b\\)。这里的\\(a\\)被称为底数,\\(b\\)被称为真数,\\(x\\)被称为对数。
三、对数函数的图像
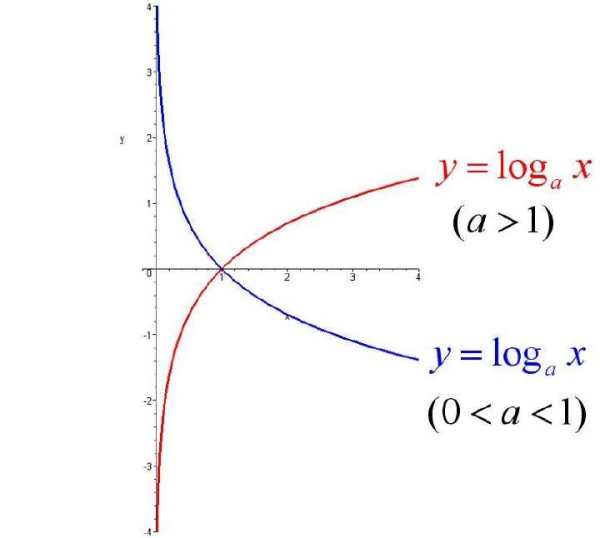
对数函数的图像非常独特,它是一条平滑的曲线。下面,我们就从几个角度来欣赏这条曲线的美。
1. 横轴和纵轴
对数函数的图像横轴表示的是对数函数的自变量\\(x\\),纵轴表示的是函数值\\(y\\)。在\\(x > 0\\)的范围内,对数函数的值域是全体实数。
2. 单调性
对数函数在\\(x > 0\\)的范围内是单调递增的。也就是说,随着\\(x\\)的增大,\\(y\\)也会增大。这是因为对数函数的底数\\(a\\)大于1时,随着\\(x\\)的增大,\\(a^x\\)也会增大,从而使得\\(y\\)增大。
3. 渐近线
对数函数的图像有两条渐近线,分别是\\(x = 0\\)和\\(y = 0\\)。当\\(x\\)趋近于0时,\\(y\\)会趋近于负无穷;当\\(y\\)趋近于0时,\\(x\\)会趋近于正无穷。
4. 特殊点
对数函数图像上还有一些特殊点,比如\\(x = 1\\)时,\\(y = 0\\);\\(x = 0\\)时,\\(y\\)趋近于负无穷。这些特殊点可以帮助我们更好地理解对数函数的性质。
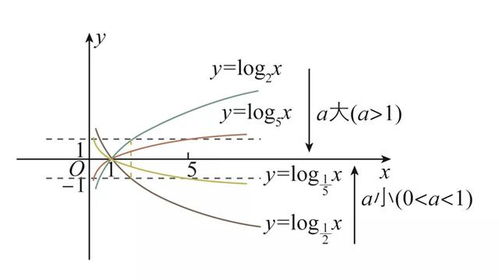
5. 底数的影响
对数函数的底数\\(a\\)对图像的形状有很大影响。当\\(a > 1\\)时,图像呈现上升趋势;当\\(0 < a < 1\\)时,图像呈现下降趋势。此外,底数越大,图像越陡峭。
四、对数函数的应用
对数函数在现实生活中有着广泛的应用。比如,在物理学中,对数函数可以用来描述放射性物质的衰变;在生物学中,对数函数可以用来描述种群的增长;在经济学中,对数函数可以用来描述市场需求的增长。
对数函数的图像就像一幅美丽的画卷,充满了神秘和魅力。通过了解对数函数的图像,我们可以更好地理解这个神奇的世界。所以,下次当你看到对数函数时,不妨停下脚步,欣赏一下它的美丽吧!
相关
-
2023城乡居民医疗保险,2023年城乡居民医疗保险政策解读与展望详细阅读

你知道吗?2023年的城乡居民医疗保险政策又有了新变化,这可是关系到咱们每个人的大事情呢!今天,我就来给你详细说说这个话题,让你对2023年的城乡居民医疗保险有个全面的认识。一...
2025-07-10 228
-
娱乐圈柳岩爆料视频大全,揭秘明星幕后故事详细阅读

娱乐圈柳岩爆料视频大全:揭秘那些不为人知的幕后故事亲爱的读者们,你是否曾好奇娱乐圈那些光鲜亮丽的明星们背后,是否隐藏着不为人知的秘密?今天,就让我带你走进娱乐圈,揭开柳岩爆料视...
2025-07-06 238
-
北京雪场,畅享冬日滑雪盛境的冰雪乐园详细阅读

哇,你有没有想过,当北京的冬天遇上滑雪,会擦出怎样的火花?想象白雪皑皑的山坡,你穿着轻盈的滑雪板,从山顶飞驰而下,那种畅快淋漓的感觉,简直让人无法抗拒。今天,就让我带你走进北京...
2025-07-06 226
-
整顿娱乐圈爆料文案短句,揭秘幕后黑幕!详细阅读

最近娱乐圈可是热闹非凡呢!各种爆料、绯闻层出不穷,让人眼花缭乱。今天,就让我带你一起深入挖掘这些娱乐圈的幕后故事,看看那些让人瞠目结舌的爆料文案短句吧!一、明星恋情曝光娱乐圈的...
2025-07-05 230
-
北京动物园复园,探秘动物新家园详细阅读

哇哦,你知道吗?北京动物园复园啦!这个曾经陪伴我们无数欢乐时光的地方,终于又焕发了勃勃生机。今天,就让我带你一起走进这个充满活力的动物园,感受一下它的新面貌吧!一、复园背后的故...
2025-07-05 226
-
对数函数的图像,图像解析与奥秘揭示详细阅读
你知道吗?在数学的世界里,有一种神奇的函数,它就像一个魔法师,能将复杂的数字变得简单易懂。它就是——对数函数!今天,就让我带你一起探索对数函数的图像,看看它那独特的魅力吧!一、...
2025-07-04 225
-
菜瓜最新事件爆料,揭秘背后惊人真相详细阅读

最近网络上可是炸开了锅,菜瓜的最新事件爆料成了大家茶余饭后的热门话题。你有没有听说?今天,我就来给你详细扒一扒这个让人津津乐道的新闻。菜瓜事件背景说起菜瓜,可能很多人都不陌生...
2025-07-04 253
-
我有一座天地钱庄,揭秘“我有一座天地钱庄”的传奇故事详细阅读

我有一座天地钱庄想象你站在一座古老而神秘的门楼下,门楼上方镌刻着“天地钱庄”四个大字,金光闪闪,仿佛在诉说着千年的故事。这就是我的天地钱庄,一个隐藏在繁华都市中的金融宝藏。钱庄...
2025-07-04 234
